오버샘플링(Oversampling)은 필요한 샘플링 개수보다 더 많은 샘플링을 수행하고 평균을 하는 기법이다. 예를 들면, 1초에 100개의 샘플링이 필요할 때 1초에 400개를 샘플링하고 4개 샘플마다 4개 샘플을 평균하여 100개 샘플을 계산한다.
오버샘플링을 하면 ADC의 해상도(Resolution)이 올라가는 효과를 얻을 수 있다.
향상되는 ADC의 해상도는 다음 식과 같다.
여기에서 n는 향상되는 ADC 비트, N은 오버샘플링하는 개수이다.
예를 들면, 100개 샘플링이 필요할 때 400개 샘플링으로 오버샘플링 한다면, N은 4이고 n은 1이 된다. 즉, ADC에서 1비트 만큼 해상도가 향상된다. 10비트 ADC에서 11비트 ADC의 해상도를 얻을 수 있다.
MA (Moving Average) 필터와 비슷하지만 조금 다르다. MA 필터는 400개 샘플 입력일 때 400개 샘플이 출력이 되지만, 오버샘플링은 400개 샘플 입력에 100개 샘플이 출력된다.
오버샘플링을 수행할 때 입력되는 신호는 x + e 이다. x는 원 신호이고 e에 원 신호에 섞여 있는 노이즈 이다. N개의 오버샘플링을 수행하면 다음 식과 같은 결과를 얻을 수 있다. 원 신호 x는 그대로 이지만 노이즈 e는 N으로 평균 된다. 노이즈가 평균이 0인 정규 분포를 이룬다면 N이 증가함에 따라 분산은 감소하게 된다.
오버샘플링은 확률적인 특성을 가진다. 해상도가 1인 ADC를 4번 오버샘플링하여 해상도를 0.5으로 향상 시킨다고 해도 확률적으로 낮을 뿐이지 1의 AD 변환 오차가 발생할 수도 있다. 즉, 10bit ADC를 사용하여 오버샘플링하는 것보다 11bit ADC를 사용하는 것이 더 정확한 측정을 할 수 있다.
오버샘플링은 MA 필터와 기본적으로 동일한 동작을 하기 때문에 MA와 유사한 주파수 응답특성을 가진다. 즉, 주파수에 따라 게인이 변하기 때문에 이에 대한 보상을 해야 한다.
'전자공학' 카테고리의 다른 글
| 정전용량식 근접센서의 원리 (0) | 2017.10.05 |
|---|---|
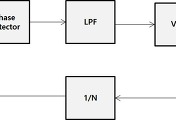
| PLL (Phase-Locked Loop) 이해 (0) | 2017.10.03 |
| IEC 모터 듀티 (0) | 2017.09.25 |
| 전선 색깔 규정 (1) | 2017.09.25 |
| 모터 스펙의 이해 (0) | 2017.09.21 |




댓글